布隆过滤器实现原理,高效数据去重与近似计数原理解析

探索布隆过滤器的奇妙世界：深入理解其实现原理

想象你正在浏览一个巨大的在线购物网站，突然发现某个商品被推荐了无数次。你好奇这个推荐系统是如何工作的？其实，背后可能隐藏着一个神奇的数字工具——布隆过滤器。这个看似复杂的算法，却以惊人的效率解决了海量数据的存储和查询难题。今天，就让我们一起深入探索布隆过滤器的实现原理，看看它是如何用数学的魔法，在数据的世界里扮演着\过滤器\的角色。

布隆过滤器的诞生故事

布隆过滤器是由布隆兄弟于1960年发明的一种概率型数据结构。这个发明最初是为了解决计算机存储空间有限的问题，当时计算机的内存和存储成本非常高昂。布隆兄弟创造了一种巧妙的方法，用极小的空间存储大量数据，同时允许一定的误判率。这种\妥协\的思路，让布隆过滤器在数据存储领域大放异彩。

有趣的是，布隆过滤器的发明源于一个实际需求。当时，布隆兄弟正在研究如何高效地检测邮件中的垃圾邮件，他们发现传统的黑名单方法既占用空间又不够灵活。于是，他们设计了一种概率型数据结构，可以在几乎不占用额外空间的情况下，判断一封邮件是否可能是垃圾邮件。这个想法的巧妙之处在于，它接受了一定程度的\假阳性\，但完全避免了\假阴性\——也就是说，它可能会错误地标记一封正常邮件为垃圾邮件，但绝不会漏掉一封真正的垃圾邮件。

布隆过滤器的核心结构

当你第一次看到布隆过滤器的代码或数学定义时，可能会觉得它相当复杂。但实际上，它的核心结构非常直观。想象一个巨大的位数组（bit array），就像一个由无数个开关组成的数字迷宫。每个开关都有两种状态：开（1）和关（0）。布隆过滤器使用多个哈希函数（hash functions）来操作这个位数组。

具体来说，当你想要添加一个元素到布隆过滤器中时，系统会使用多个不同的哈希函数，将这个元素转换成不同的索引位置。系统会将这些位置的开关全部\打开\（设置为1）。这个过程就像是在数字迷宫中留下多个标记，每个标记都指向不同的开关。

当你想要检查一个元素是否存在于布隆过滤器中时，系统同样会使用这些哈希函数计算索引位置。如果所有计算出的位置都是\开\状态，那么系统会告诉你这个元素\可能存在\。但如果任何一个位置是\关\状态，那么可以确定这个元素绝对不存在。

这个设计非常巧妙，因为它利用了概率论中的\交集\概念。即使多个哈希函数可能会将不同的元素映射到同一个位置，但只要有一个哈希函数没有将元素映射到某个位置，那么这个元素就不可能存在于布隆过滤器中。

哈希函数的选择与平衡

布隆过滤器的性能很大程度上取决于哈希函数的选择。理论上，如果使用足够多的哈希函数，布隆过滤器的误判率可以降到非常低的水平。但实际上，哈希函数的数量需要精心选择，过多或过少都会影响性能。

一个常见的做法是使用2到4个哈希函数。每个哈希函数都应该能够均匀地将输入数据映射到位数组的索引上。如果哈希函数不够好，可能会导致多个元素被映射到相同的索引位置，从而增加误判率。反之，如果哈希函数数量不足，位数组中\关\状态的位置会过多，也会增加误判。

有趣的是，布隆过滤器中的哈希函数不需要是完美的，也不需要是加密安全的。它们只需要能够提供足够均匀的分布即可。这种灵活性使得布隆过滤器非常实用，因为简单的哈希函数通常比复杂的加密哈希函数更容易实现，也更快。

在实际应用中，开发人员可能会根据具体需求调整哈希函数的数量和类型。例如，在处理大量数据时，可能会使用多个不同的哈希函数族，每个族包含多个哈希函数，以进一步提高分布的均匀性。

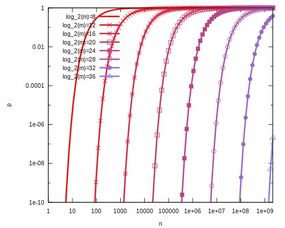
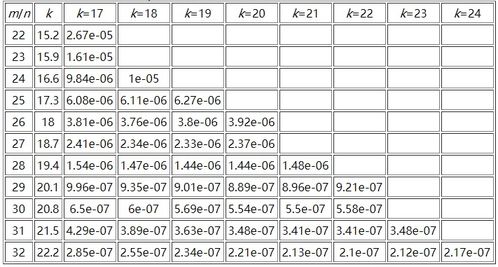
误判率与空间效率的奇妙平衡

布隆过滤器最迷人的特性之一是它能够在空间效率和高准确性之间取得平衡。通过调整位数组的大小和哈希函数的数量，可以控制误判率。这个关系可以用一个简单的公式来描述：

误判率 ≈ (1 - e^(-kn/m))^k

其中：

- n 是位数组的大小

- k 是哈希函数的数量

- m 是元素数量

- e 是自然对数的底数

这个公式揭示了布隆过滤器中几个关键参数之间的关系。当你增加位数组的大小或哈希函数的数量时，误判率会下降。但增加位数组大小的影响更大，因为哈希函数数量增加会更快地达到饱和状态。

这个平衡非常重要。如果追求极低的误判率，可能会需要非常大的位数组，这会抵消