树形布隆过滤器,高效数据检索与去重利器

探索树形布隆过滤器的奇妙世界

你有没有想过，在浩瀚的互联网数据海洋中，如何高效地判断某个元素是否存在于某个集合里？传统的数据结构如哈希表、平衡树等虽然功能强大，但在面对海量数据时，它们的性能会逐渐下降。这时，一种名为\树形布隆过滤器\的神奇数据结构就闪亮登场了。它就像一位技艺精湛的侦探，能在极短的时间内告诉你某个元素是否可能存在于某个集合中，而且它还特别擅长节省空间。今天，就让我们一起深入探索树形布隆过滤器的奇妙世界，看看它是如何工作的，以及它在现实世界中有哪些惊人的应用。

树形布隆过滤器的诞生背景

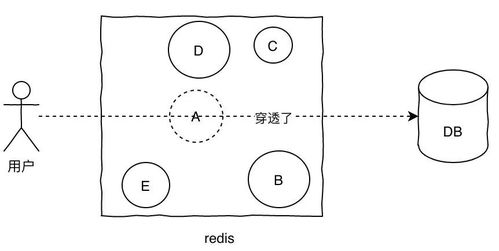
想象你正在经营一家大型电商平台，每天有数以亿计的商品被浏览和搜索。当你想要检查某个商品是否已经存在于你的数据库中时，传统的查找方法可能会让你望而却步。因为随着数据量的不断增长，查找效率会越来越低，系统响应时间也会越来越长。这时，布隆过滤器就应运而生了。

布隆过滤器是由布隆（Bloom）和布特（Burt）在1970年提出的，它是一种空间效率极高的概率型数据结构，可以用来测试一个元素是否是一个集合的成员。布隆过滤器有一个巨大的优点：它永远不会将不存在于集合中的元素误判为存在，但可能会将存在元素误判为不存在。这种\假阴性\的错误率是可以控制的，而且随着空间的减小，错误率会相应增加。

普通的布隆过滤器有一个致命的缺点：它不支持删除操作。一旦一个元素被加入，它就永远存在于布隆过滤器中，即使你想要删除它，布隆过滤器也无法区分这个元素是曾经存在但现在被删除了，还是从一开始就不存在。这就是树形布隆过滤器诞生的原因——它在布隆过滤器的基础上，巧妙地解决了删除操作的问题。

树形布隆过滤器的内部结构

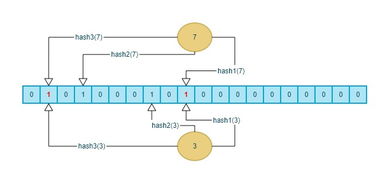
树形布隆过滤器可以看作是一个多层的布隆过滤器网络。在最底层，有多个独立的布隆过滤器，每个布隆过滤器负责检查一个特定的子集。当你要检查一个元素是否存在于某个集合中时，这个元素会被逐层传递，经过每一层的布隆过滤器检查。如果所有层的布隆过滤器都判断该元素存在，那么最终结果就是\存在\；如果任何一层的布隆过滤器判断该元素不存在，那么最终结果就是\不存在\。

这种多层结构的设计非常巧妙。每一层的布隆过滤器都使用不同的哈希函数，这样就可以减少哈希碰撞的概率。同时，每一层的布隆过滤器都只负责检查整个集合的一个子集，这样就可以大大减少单个布隆过滤器的规模，从而节省空间。

树形布隆过滤器的核心思想是\分而治之\。它将一个大集合分解为多个小集合，然后对每个小集合使用独立的布隆过滤器。这样，当你要检查一个元素是否存在于整个集合中时，你只需要检查它是否存在于所有的小集合中。如果它存在于所有小集合中，那么它很可能存在于整个集合中；如果它不存在于任何一个小集合中，那么它肯定不存在于整个集合中。

树形布隆过滤器的关键特性

树形布隆过滤器最令人惊叹的特性之一是它的可扩展性。随着数据量的增长，你可以通过简单地添加更多的布隆过滤器来扩展树形布隆过滤器，而无需对现有结构进行任何修改。这种水平扩展的能力使得树形布隆过滤器非常适合用于处理海量数据。

另一个令人印象深刻的特点是它的高效性。树形布隆过滤器的查询时间复杂度为O(1)，这意味着无论数据量有多大，查询时间都保持不变。这与传统数据结构的查询时间随数据量增长而增长形成了鲜明对比。

此外，树形布隆过滤器还具有非常高的空间效率。相比于传统的数据结构，它可以节省大量的存储空间，尤其是在处理海量数据时。这种空间效率的提升来自于布隆过滤器本身的高效设计，以及树形结构的进一步优化。

树形布隆过滤器的实际应用

树形布隆过滤器在现实世界中有着广泛的应用，尤其是在网络领域。例如，在内容分发网络（CDN）中，树形布隆过滤器可以用来快速判断一个请求的资源是否已经存在于缓存中。如果存在，CDN可以直接从缓存中返回资源，从而大大减少延迟；如果不存在，CDN需要从源服务器获取资源，然后缓存起来以备后续使用。

在搜索引擎中，树形布隆过滤器可以用来快速判断一个网页是否已经被索引过。如果已经索引过，搜索引擎可以直接从索引中返回结果；如果还没有索引过，搜索引擎需要爬取这个网页，然后进行索引。

另一个有趣的应用是在垃圾邮件过滤中。邮件服务器可以使用树形布隆过滤器来快速判断一封邮件是否可能是垃圾邮件